Damping
We carried out a precise evaluation of quality factor Q at varying pressure. This theory can be applied to microphones and gyroscopes. Typically, by varying pressure the quality factor changes according to a curve as shown in the following figure. Different source of damping are actually involved at the different pressures.
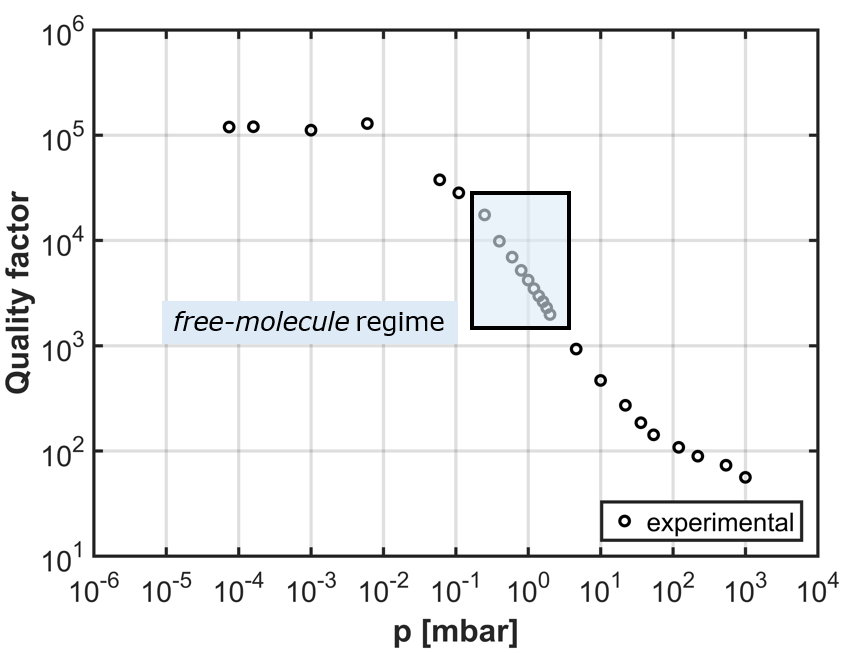
Quality factor at varying pressure
At very low pressure (<0.01 mbar) solid/surface damping is dominant (e.g. thermoelasticity). The effect of thermoelastic loss mechanism on dissipation for small-scale mechanical devices is evaluated by means of theoretical study and computational finite element models.

FE model of the clamped-clamped resonator
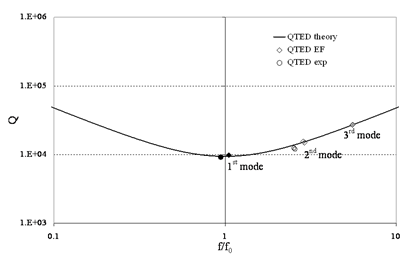
Quality factor of clamped-clamped beams versus relative frequency, experimental results from Roszhart 1990
The classical thermoelastic analysis is unable to interpret the size effect recently evidenced in resonators when the dimensions become very small, below several microns. To improve the prediction of the quality factor based on thermoelstic dissipaition in the case of very thin resonators, we propose a non-local coupled thermoelastic model.
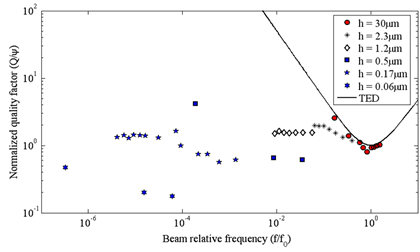
Dimensional effects: normalized quality factors resulting by various experiments are plotted versus beam relative frequency and compared to the Zener’s thermoelastic curve (data form Le Foulgoc et al. 2006, Yang et al. 2002, Yasumura et al. 2000)
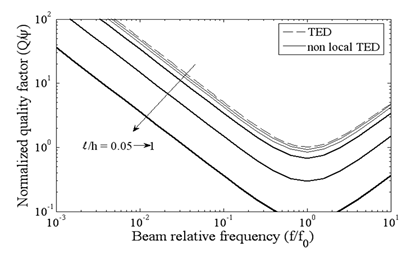
Reduction of Q is achieved by nonlocal computations for different l/h ratios
For sub-micron and nano-resonators, several causes of additional dissipation, not yet exhaustively investigated, come into play. Intrinsic dissipation of thin coating films and surface loss may become relevant at very small scales. We focussed on the effect of the presence of superficial layers, with different thermo-mechanical properties, on the quality factor of micro-beams and we included thermally imperfect interfaces between layers: this means that a temperature jump is involved at the interface, with consequences on the thermal behaviour of the beam and on the overall dissipation. In particular for Si beams covered by a thin oxide layer, varying the thermal properties of the interface one observed a significant dissipation peak which increases with the oxide thickness.
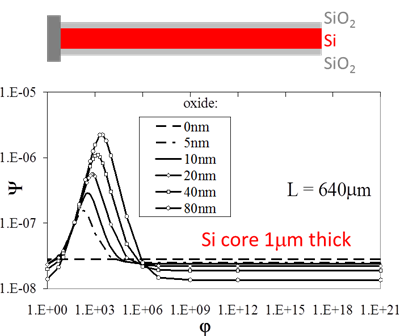
Thermoelastic damping vs. interface dissipation parameter for oxidized resonators
When the pressure p is in the range 0.01 mbar < p < 100 mbar the fluid damping is dominant. At lower pressures the collisions between molecules can be neglected. This regime, known as free-molecule, can be described through deterministic approaches based on the collision-less Boltzmann equation.
A numerical model for the prediction of gas damping occurring in MEMS working in near vacuum conditions has been developed and experimentally validated. The model is based on boundary integral equations (BIE) approach. A simplified, fast and operative simulation tool has been developed to obtain a sufficiently accurate estimate of damping coefficient for many typical configurations of MEMS.
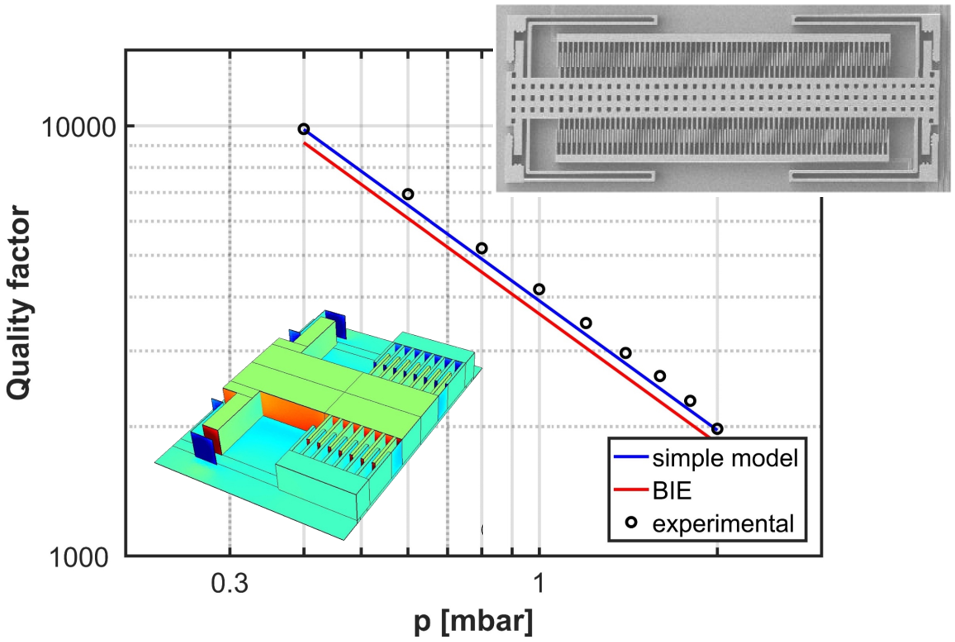
Quality factor at varying pressure in the free-molecule regime
We assume that a complex MEMS can be considered as a collection of uncoupled elemental blocks for which an accurate estimation of the gas damping is obtained once for all.
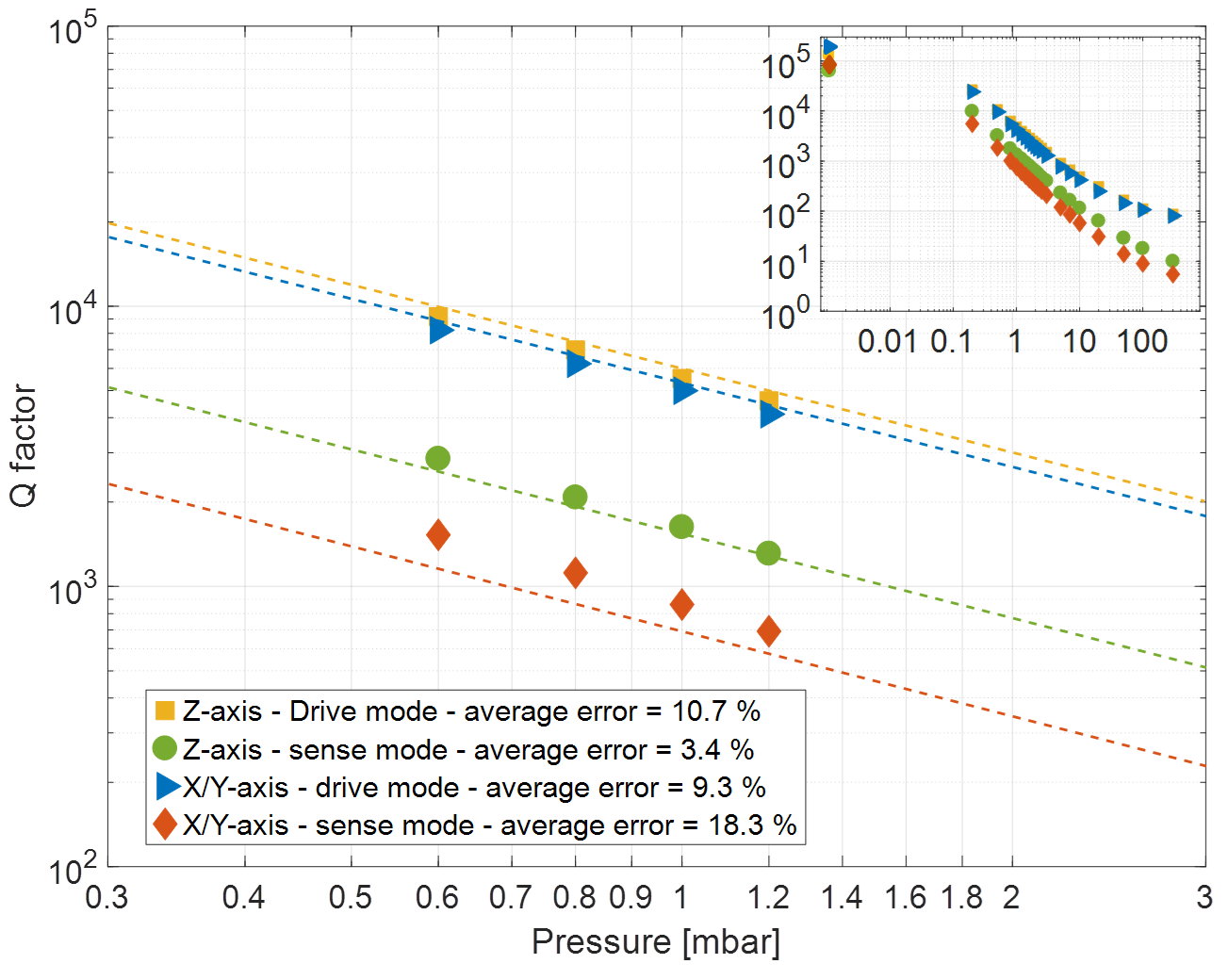
Quality factor vs. pressure for typical MEMS structures
When the ambient pressure is approached, if the gap between the MEMS parts are very small, the fluid finally can be considered as a continuum, but stick boundary conditions must be applied. Our code based on integral equations can correctly capture the physical response of the system.
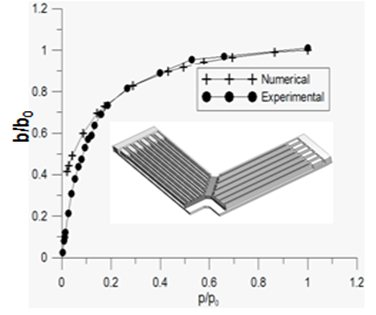
Damping coefficient vs. pressure for a MEMS structure
